【印刷可能】 重複組み合わせ 公式 203075-重複組み合わせ 公式 なぜ

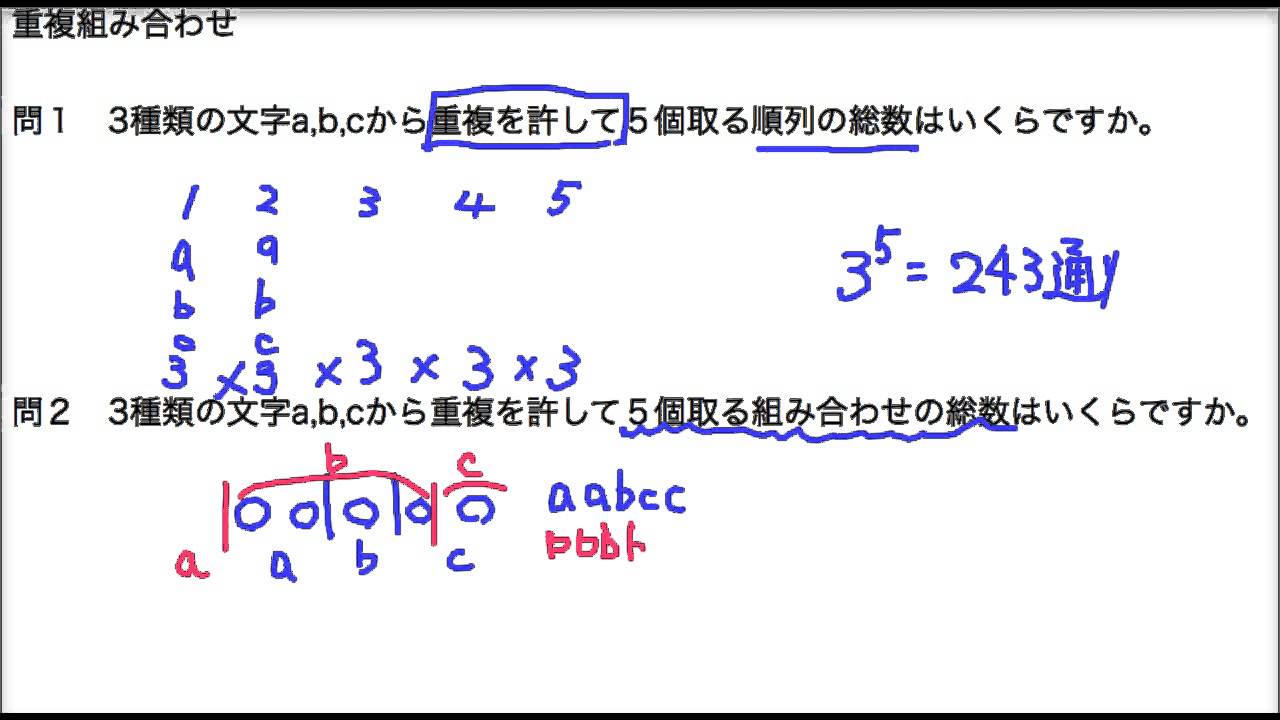
詳しくは『 組み合わせとは？ 絶対に知っておくべき 2 つの公式と計算のパターン 』で解説しています。 重複組み合わせ（復元抽出） 重複組み合わせは、同じ要素を何回使っても良い場合（復元抽出の場合）の組み合わせ これは、この組み合わせの数の公式を使う事で 5 c 2 ＝5×4÷2＝10通り と求めることができます。 下のように表にして考えると「並びだけが違う、組み合わせとして見たら同じものが1セットにつき 2！＝2 個ずつ存在する」のが分かりやすくなります。 公式を理解していないと、混乱するか、解くまでに時間を浪費してしまいます。公式をしっかり覚えて準備をしておきましょう。 では早速次の5問を解いてみましょう。 重複順列、重複組み合わせ、円順列の問題 問題 1：

順列と組み合わせの違いと見分け方 公式や練習問題 受験辞典

重複組み合わせ 公式 なぜ

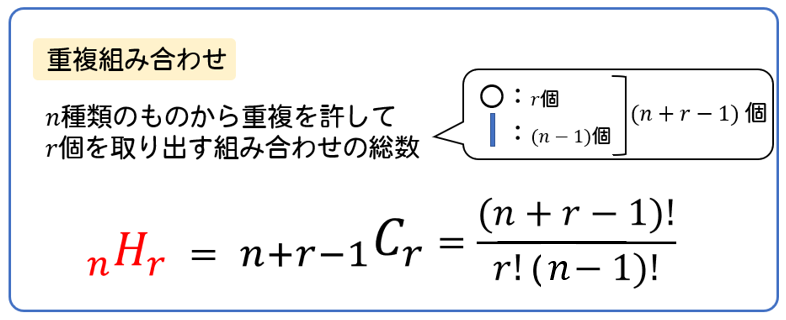
重複組み合わせ 公式 なぜ-重複組合せ 入力boxの横にあるヒントは「n≧r≧0」ではなく「r≧n≧0」なのでは？ 別解の計算時間省略のため。 種類のある商品の組み合わせを知りたかった。 このサイトが存在する事に感謝。 現実の素粒子の選択で、Down QuarkとUp Quarkの二つで、電子（d×重複組み合わせの公式 上の例では3種類の果物の中から4個選ぶという計算をしました。 その結果、 6 C 4 という式ができました。 これは 4 ( 3 − 1) C 4 と表せます。 左側は、4個の選ぶべきマスに加えて31個の仕切りが入り、計4 (31)の場所ができた、という意味です。 これをより一般化した公式は次のようになります。 n r − 1 C r また、この重複組み合わせの計算を特に H として表すことも

重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ

どの果物も1個以上選ぶという条件で，りんご，みかん，なし，3種類の果物から7個選ぶ方法は何通りありますか？ 3種類の果物から7個とる重複組み合わせを考えて 9 C 7 = 9 C 2 = 36 通りだね！ 重複組み合わせの公式は合っていますが，問題をよく見てください。 重複組み合わせで考えたときは，選ばない果物があってもよかったですね重複組合せ n H r の公式を作るには 1 重複順列の総数から割り算で求めることはできない まず思いつくのは，順列と組合せの対応ですが 順列 n P r ÷r！ → 組合せ n C r のように，順列をr！ で割ると組合せになりますが，重複順列 n Π r と重複組合せ n H r の関係は単純ではありません これは，上の例のように重複組合せの中身ごとに並べ方の総数が変わり， 倍率が一定のr！ にならない からです 8 − ( x y z) = w 8 − ( x y z) = w と、新しい変数 w w を定める。 すると仮定より、 w ≧ 0 w ≧ 0 であり、また x y z w = 8 x y z w = 8 となる。 したがって、 4 4 種類から 8 8 個取る重複組合せになるので、 4 H 8 = 11 C 8 = 11 C 3 = 165 ( 通 り) 4 H 8 = 11 C 8 = 11 C 3 = 165 ( 通 り) (解答終了) どんな問題になっても「重複組合せの基本パターンに帰着させる」 これを

 組戻しには 振込組戻手数料864円（消費税込）がかかります 。 ただし、PayPay銀行（旧：ジャパンネット銀行）の公式HPにもあるように 一度相手方の口座に入ってしまったお金は、受取人（口座名義人）の了承無く返還してもらうことが出来ません 。 金融1 総和の公式集 ※何の断りも無ければ、m,n は自然数とします。 1m 次式の総和 ∑n k=1 k(k 1)(k 2)(k m 1) = n(n1)(n2)(nm) m1 または、 ∑n k=1 km 1Pm = nmPm1 m1 2m 重のシグマ ∑n a1=1 ∑a1 a2=1 ∑a2 a3=1 a∑m 1 am=1 1 = n(n1)(n2)(nm 1) m! 数学IAIIB 差をつける自宅学習を始めよう ここでは重複を許して取る組合せについて説明します。 「同じものを繰り返し取っても良い」という条件によって，用意されている種類より多くの個数を取ることもできるようになります。 また，ここで

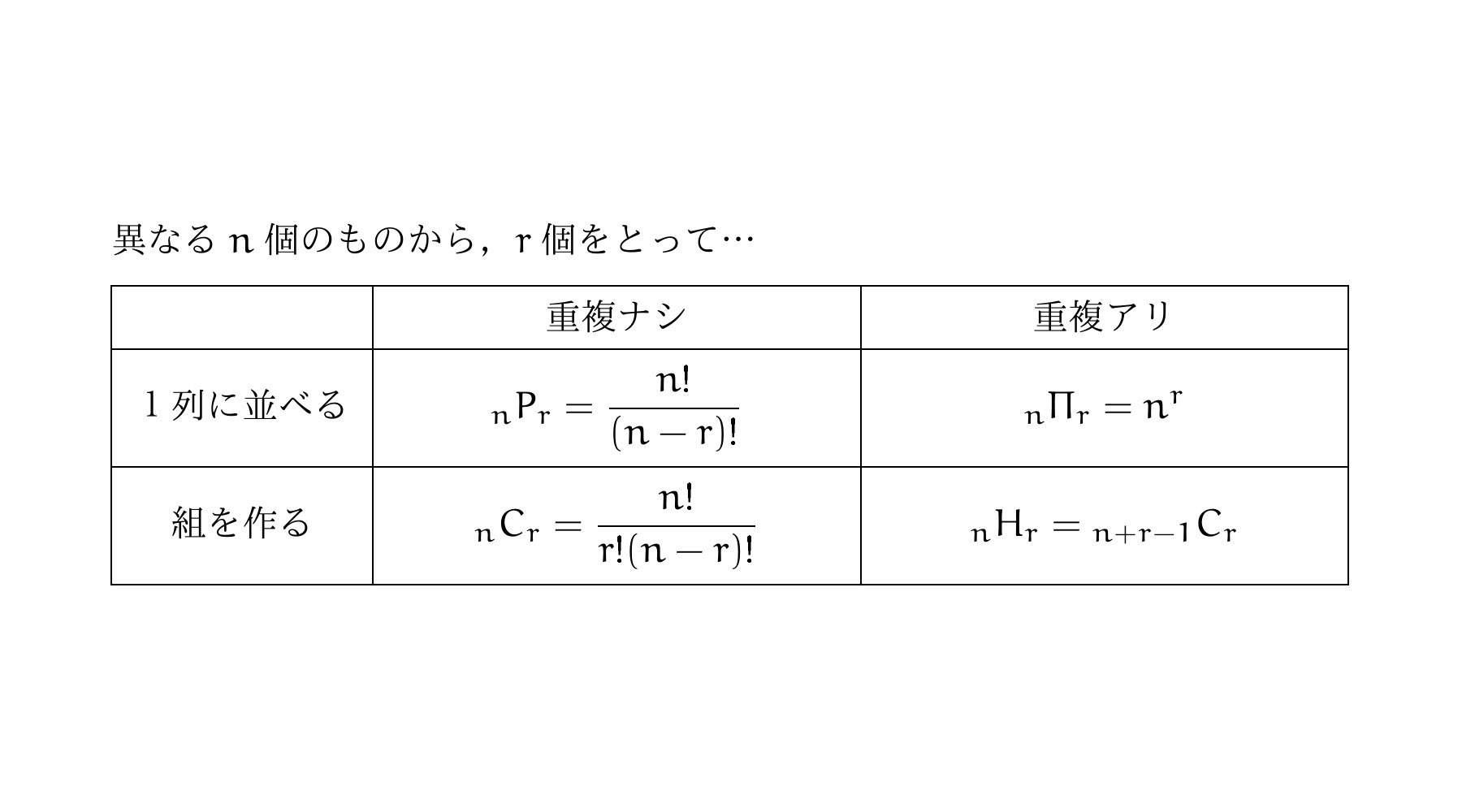
 重複順列の考え方を応用して，組分けの問題を解いてみましょう． 例題 赤，青，黄，緑，紫色の 5 5 つの球がある． (1) 5 5 つの球を 2 2 つの箱 X,Y X, Y にいれる方法は何通りあるか．ただし，ひとつの球も入っていない箱があってもよいとする． (2) 5 5 つの組み合わせ（C）の公式と順列・重複組み合わせの計算方法 順番を考慮しない場合が組み合わせ 同じものを含む順列の計算 重複組み合わせの計算方法 重複組合せとは 異なる n n 個のものから異なる r r 個を取り出す組合せの総数は nCr n C r でした． ( →組合せの基礎) では，異なる n n 個のものから， 重複を許して r r 個取り出す組合せの総数はいくつになるでしょうか． これを， n n 個から r r 個選ぶ 重複組合せ といいます． たとえば， A,B,C,D A, B, C, D の 4 4 種類の記号から，重複を許して 3 3 個選ぶ組合せの総数はつぎのように，

重複順列の応用問題 組み分けの問題 あうるさんの杜

組み合わせ C とは 公式や計算方法 は何通り 受験辞典

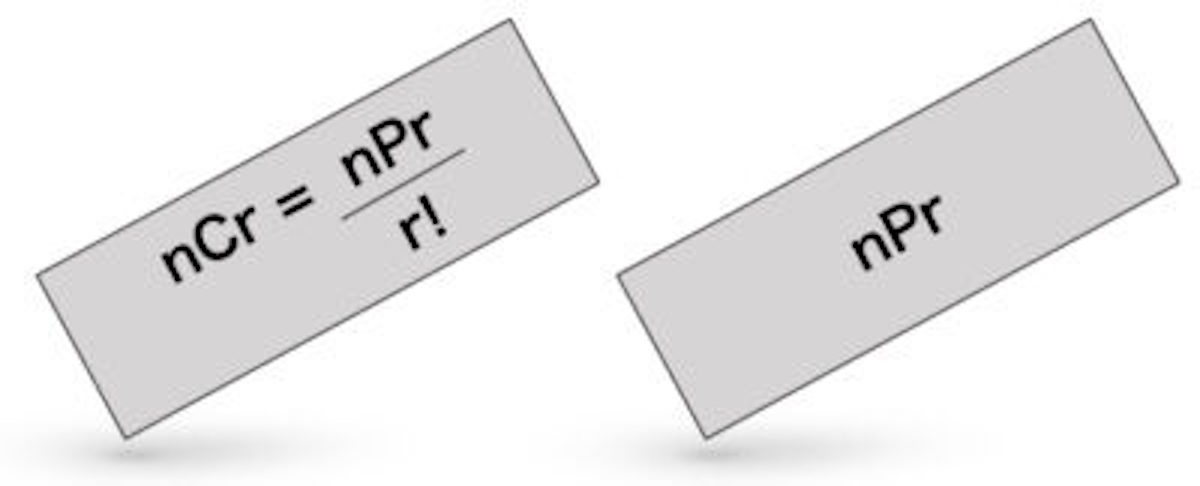
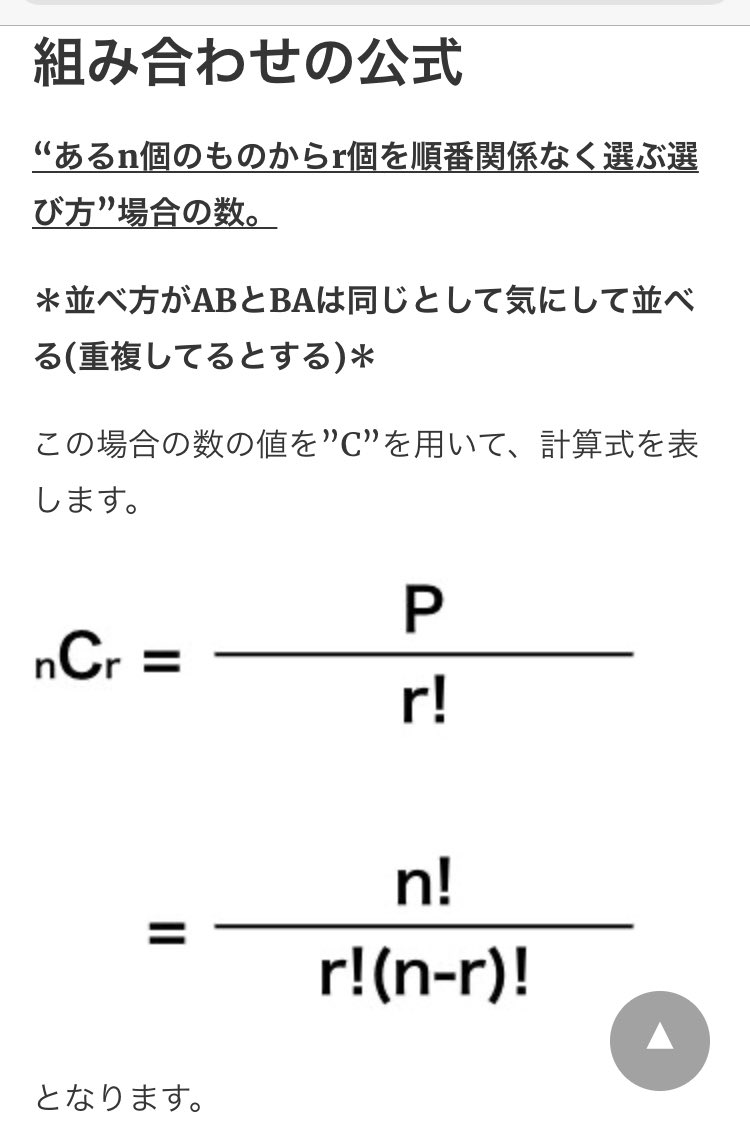
重複組み合わせでは， 選ばれないものがあって良い場合 選ばれないものがあってはならない場合 の2種類を考えることが多い．それぞれどのような考え方をするのか理解する． 重複組み合わせの公式 問題のの考え方と同様にして，次の公式が分かります． 重複組み合わせ n 種類のものから全部で r 個選ぶ場合の数は， 選ばれないものがあっても良い場合は ( n r − 1)! これらが”順列”の計算であり、公式となります。 組み合わせの公式 “あるn個のものからr個を順番関係なく選ぶ選び方”場合の数。 ＊並べ方がABとBAは同じとして気にして並べる(重複してるとする)＊ この場合の数の値を”C”を用いて、計算式を表します。N C r = n P r r!

順列と組み合わせの違いと見分け方 公式や練習問題 受験辞典

場合の数３８ 重複組合せの導入３ 怜悧玲瓏 高校数学を天空から俯瞰する

= nm 1Cm = nHm 3 数列の積の総和 ∑n k=1 akbk = an ∑n k=1 bk ∑n k=1 (ak ak 1)k組み合わせcの計算のやり方を簡単にサクッと解説するぞ！ 平行四辺形は何個ある？考え方を解説！ 組み分けの場合の数の求め方・考え方をイチから解説！ なぜ？同じものを含む順列の公式と使い方について問題解説！ ←今回の記事;( n − 1)!

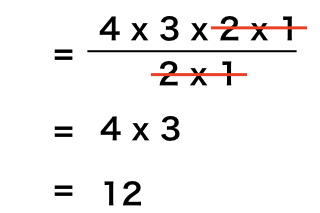
組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather

Amazon Com Mathematics Formula For Difficult High School Passes Do You Answer In 10 Seconds Math Formula Japanese Edition Ebook Yoruhayonetaro Kindle Store

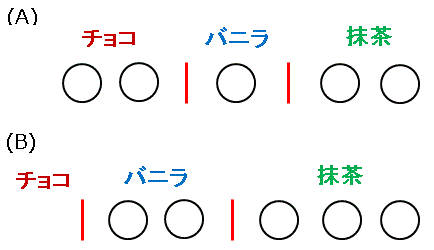
 この場合は次のように考えましょう。 (2) → x=4,y=0,z=5 (3) → x=0,y=0,z=9 x,y,zが0でもOKなので、仕切り（｜）が連続しても構わないのです。 では、 (1)～ (3)の絵をまとめて式で表すとどうなるでしょうか？ 9個の と2個の仕切り（｜）をそれぞれ同じものと考えて、 同じものを含む順列 の公式を適用します。 同じものを含む順列の公式は次の通りです。 n個の 重複組み合わせの公式 重複組み合わせ 異なる 個のものから重複を許して 個を選ぶ組み合わせの総数は、 二項定理 組み合わせの考え方を使って多項式のべき乗を展開できます。 二項のべき乗で成り立つ等式を「二項定理」、複数の項のべき乗で成り立つ等式を「多項定理」といいます。 二項定理 一般項（第 項）は 多項定理 の一般項は ただし、, , は整数で以下を満たす。 二項定理と 重複組合せの公式は nHr = (nr1)Cr でしたね。 n は食材の種類の数、r は買った食材の個数なので、この問題の場合 n = 3、r = 6です。 買った食材の個数は6個だから〇は6個 描きました。 では仕切りの数はなぜ2個なのでしょう？ それは、 2個の仕切りで3個に分割できる からです。 上で描いたように、2個の仕切りを入れることで食材を3種類に分けられていますね。 消しゴムを2回切

場合の数の数え方 P C P H 感じる科学 味わう数学

高校数学数a組み合わせまったくもって意味がわかりませんなんで重複組み合わ Yahoo 知恵袋

場合の数4｜組み合わせのnCrの求め方から性質まで攻略 場合の数5｜同じものを含むと順列の場合の数はどう変わる？ 場合の数6｜重複組み合わせは2パターンでOK！ 場合の数7｜二項定理を理解しよう！場合の数を使って導出！ 最もシンプルな重複組合せ まずは、重複組合せの中で、一番簡単な例を見てみましょう。 例題1 「A」「B」と書かれたカードが、それぞれ5枚ある。 これらから5枚選ぶ方法は何通りあるか。 選ぶ方法なので、順番は関係ありません。 「AABBA」と選ぶのとつぎに重複順列の公式と使い方を確認していきましょう。 重複順列の公式と使い方 異なる\(n\)種類のものから、重複を許して\(r\)個取り出して並べる順列を、\(n\)個から\(r\)個取る重複順列という。 重複順列では、\(r \leq n\)とは限らず、\(r \gt n\)であってもよい。

重複組合せの考え方 思考力を鍛える数学

2

 組み合わせの計算の公式は次の式になります。 組み合わせの公式 \( n \) 個のものの中から \( r \) 個取り出すときの組み合わせの総数は その後でその区別をなくす。重複して数えている分を取り除く！ この2つのプロセスで公式ができているため ！ 公式の仕組みが同じなので 、同じものを含む順列の問題は組み合わせを使って解けます。 例えば、先ほどの3つのケーキを一列に並べる問題。重複組み合わせ（復元抽出） の場合 2 つの公式を挙げます。 組み合わせ 組み合わせは以下の方法で求めることができます。 nCr = nP r r!

高校数学 重複組合せについて 数樂管理人のブログ

場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん

では, 重複組合せと対になるものは何だろうか 重複組合せの公式nHr は異なるn 個のものから重複を許してr 個選ぶときに使う この定義が難しい これも例をあげて考えてみよう 1,2,3 から重複をゆるして2 個選ぶなら, 11,12,13,22,23,33の6 通り 重複組合せの公式：nHrは今すぐ忘れるべし！ 重複組合せの解法（例題1） 丸仕切り法とは （例題1−1）典型的な「区別が付かないものを区別がつくものに分ける」問題 2番は全員最低一個もらえるという部分が違うので少しだけ先に細工をしておきます 丸仕切り法の応用編 （2−1）1≦w≦x≦y≦z≦7となる（w、x、y、z）の組は幾つあるか。 重要な別解物理公式集 初等組み合わせ 2つある数を重複可能とし、8個並べた時の並べ方数が計算できました。「重複を許した場合の順列は、単純にn^r

場合の数 Of 京極一樹の数学塾会員頁

3

 重複順列の公式の説明 1，2，3，4，5の5つの数字を使ってできる3桁の整数は全部で何個ですか？ 百の位について1~5の5通り，十の位について1~5の5通り，一の位について1~5の5通り，これらは3桁の整数1つをつくるときに続けて選ぶ (同時に起こる)のでその総数は積の法則を用いて 5 × 5 × 5 = 5 3 = 125 (個)となります。 5通りの選択を3回続けて行うから 5 3 なんだね！ 一般には n 重複組合せの公式 重複組合せの公式は、一般的に次のように表されます。 異なるn個のものから重複を許してr個のものを取り出す場合の数は n H r = nr1 C r 「重複」とは、同じものを何回も選ぶことです。 たとえば、A,B,C,D,Eの5文字から3文字を選んで文字列を作るとします。 重複NGの場合、AABやAAAを作れません。 Aを一回しか使えないからです。 一方( n − r)!

ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun

数学 忘れがちな公式 Flashcards Quizlet

重複組合せの公式と例題（玉，整数解の個数）』 高校数学の美しい物語 Michel Hort "Nombre de combinaisons et d'arrangements avec répétitions limitées" Cite webテンプレートでは accessdate= 引数が必須です。結論から言うと、組み合わせの公式は、単純に「順列を、1 組の組み合わせの中に含まれている順列の数（同じ組み合わせで並び方が異なるものの重複数）で割る」ということをしているだけです。 例として A, B, C, D の 4 つの要素から 3 つを取り出して並べる場合（順列の場合）と、取り出すだけの場合（組み合わせの場合）を考えてみましょう。 このとき順列は以下の 24 通りあります。 {ABC,

高校数学a 重複組合せの基本 Nhr X Y Z の展開式の項の種類 受験の月

2

数学 忘れがちな公式 Flashcards Quizlet

重複組合せとは 重複組合せの公式の意味 きぬごしのお受験ブログ とうふめんたるず公式ブログ

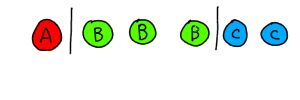
重複組み合わせは絵を描けば理解できる イラストで解説 理数白書

数学i Aチェック リピート 第7章 2順列 組合せ 6 重複組合せ Pukiwiki

重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学

重複組み合わせの問題を解くたった1つの方法とは 公式hは使用注意

大島学習塾 私は 重複組合せ の公式は 他の手法で代用できる事は知りつつ 順列 や 組合せ の公式とほぼ同等に授業で扱っています でも解答速報などでは意図的に使用を避けているような 皆さんはどうされていますか 数学 T Co

重複順列とは 基本公式と解き方を解説 高校生向け受験応援メディア 受験のミカタ

Amazon Com Mathematics Formula For Difficult High School Passes Do You Answer In 10 Seconds Math Formula Japanese Edition Ebook Yoruhayonetaro Kindle Store

1

重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学

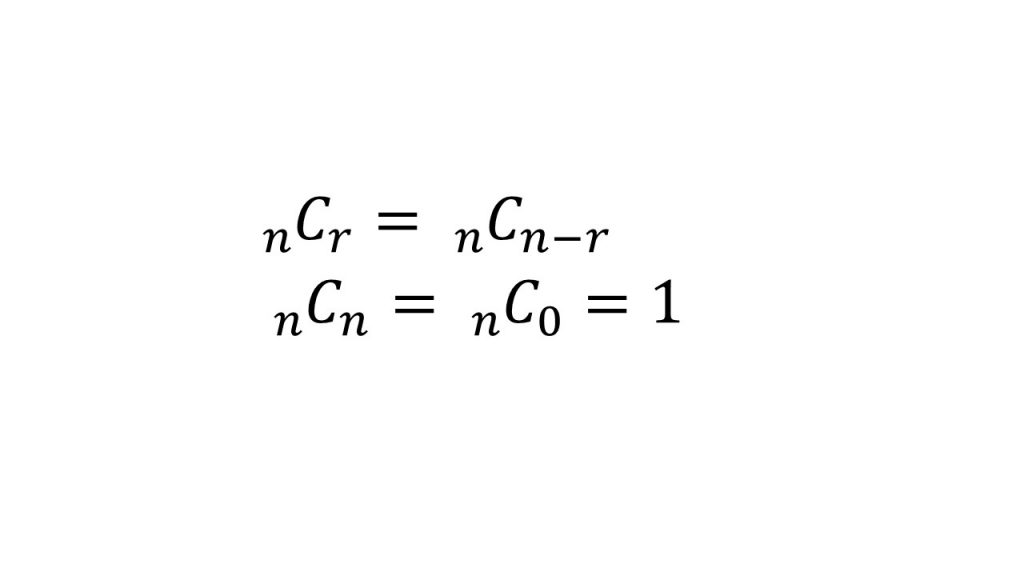
順列と組み合わせ公式 大学受験の王道

確率の問題で 重複組合せが分母になることはありますか あと 円順列の公式 Yahoo 知恵袋

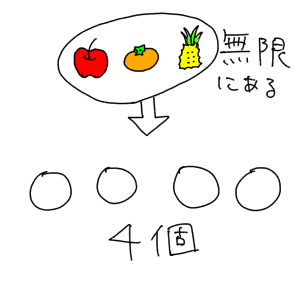
重複組み合わせは絵を描けば理解できる イラストで解説 理数白書

組み合わせ シキノート

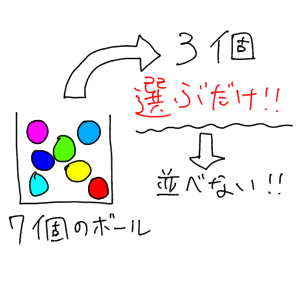
組み合わせ 並べない順列のこと 考え方と計算方法を解説 理数白書

整数問題は13パターン 京極一樹の数学塾

数学 忘れがちな公式 Flashcards Quizlet

場合の数３７ 重複組合せの導入２ 怜悧玲瓏 高校数学を天空から俯瞰する

重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ

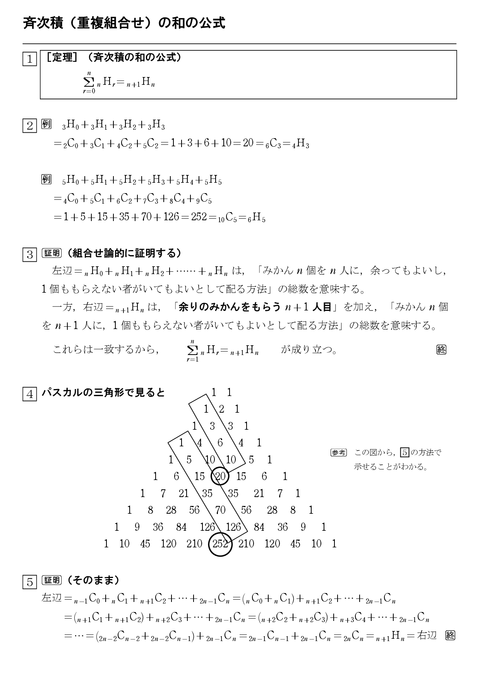
15年10月 怜悧玲瓏 高校数学を天空から俯瞰する

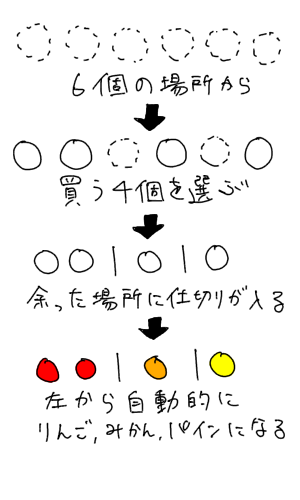
重複組み合わせは絵を描けば理解できる イラストで解説 理数白書

2

重複順列 Itパスポート出題テーマ別過去問題 平成24年度秋期 テクノロジ系 問78

場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん

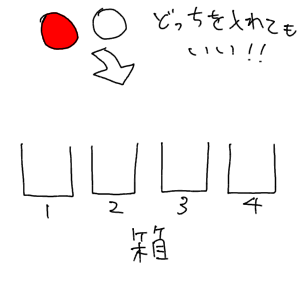
重複順列 同じものを並べられる順列 その考え方をイラストで解説 理数白書

順列 P とは 公式や計算問題の解き方 重複ありなど 受験辞典

重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学

重複組合せの考え方 思考力を鍛える数学

重複組み合わせ は２パターンを区別すればok

重複組み合わせをわかりやすく解説 公式を使えない問題も攻略しよう みみずく戦略室

組み合わせ C とは 公式や計算方法 は何通り 受験辞典

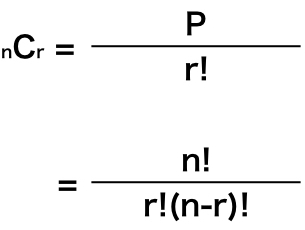
組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather

重複組合せの公式と方程式の問題 Of 京極一樹の数学塾会員頁

重複組合せとは 重複組合せの公式の意味 きぬごしのお受験ブログ とうふめんたるず公式ブログ

重複組み合わせを列挙 C 追記にpythonコード Qiita

場合の数３６ 重複組合せの導入１ 怜悧玲瓏 高校数学を天空から俯瞰する

Pisso2pm6zu2ym

場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん

組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather

重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学

3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ

重複順列の問題６選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学

組合せと重複組合せの公式 Excel Vba 数学教室

重複組み合わせ 大学受験の王道

15年10月 怜悧玲瓏 高校数学を天空から俯瞰する

重複組み合わせを完全マスター 厳選８問 ふるやまんの算数塾

重複組合せの公式と例題 玉 整数解の個数 高校数学の美しい物語

順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ

場合の数３９ 重複組合せで楽になるいいかえ 怜悧玲瓏 高校数学を天空から俯瞰する

2

重複組合せ 文章題

組み合わせ C とは 公式や計算方法 は何通り 受験辞典

重複組合せの考え方 思考力を鍛える数学

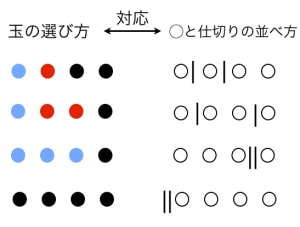
重複組合せの公式と例題 玉 整数解の個数 高校数学の美しい物語

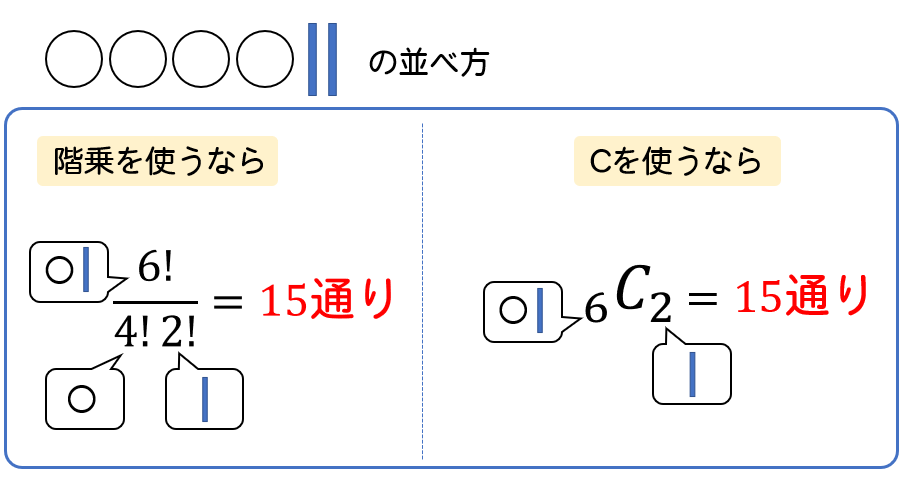
重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ

なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ

グラタン V Twitter Rt Komurazi Maki 式の計算はできるのですが なぜこの公式なのか というところが曖昧なので 英国紳士にはなれないです 昔から 計算はできるのに 正しい式を組み立てるのが苦手で T Co F2nmxefb0i Twitter

組み合わせ C とは 公式や計算方法 は何通り 受験辞典

数a 重複組合せ １個のサイコロを４回投げて出た目を順に A B C Dとする Youtube

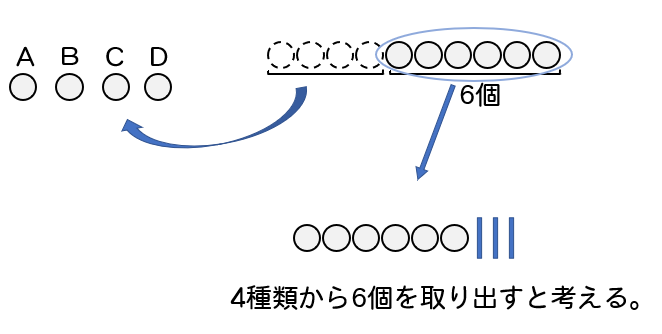
重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ

重複組合せと両替問題の公式 漸化式と母関数 Qiita

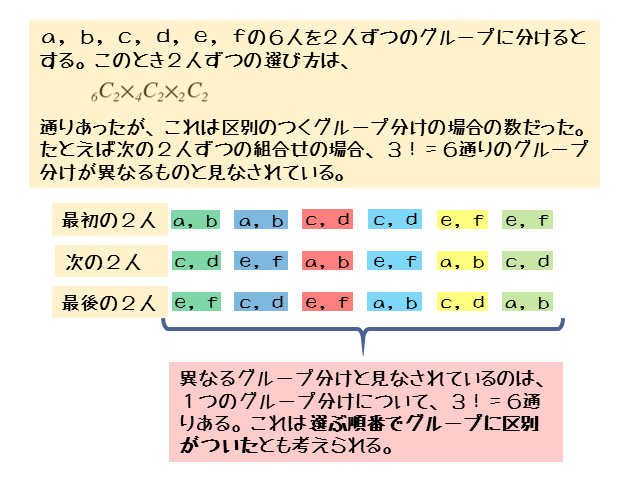
場合の数 グループ分けについて 日々是鍛錬 ひびこれたんれん

順列 P とは 公式や計算問題の解き方 重複ありなど 受験辞典

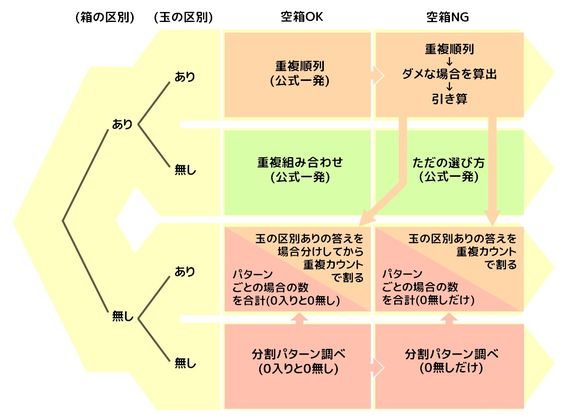
組み分け 部屋分け 問題全8パターンと解き方 数a 場合の数確率 そうちゃ S 図解英数ゼミナール

重複組み合わせの公式と証明 簡単な計算方法 ビジュアル数学 数学ａ 場合の数

重複組み合わせの公式が使えない理由を教えてください には使 Yahoo 知恵袋

5講 組合わせ 1章 場合の数と確率 問題集 高校数学a

順列組み合わせ こちら重複組み合わせの公式でいけると思う Yahoo 知恵袋

高校数学 数a １８ 組合せ 重複編 Youtube

場合の数 Of 京極一樹の数学塾会員頁

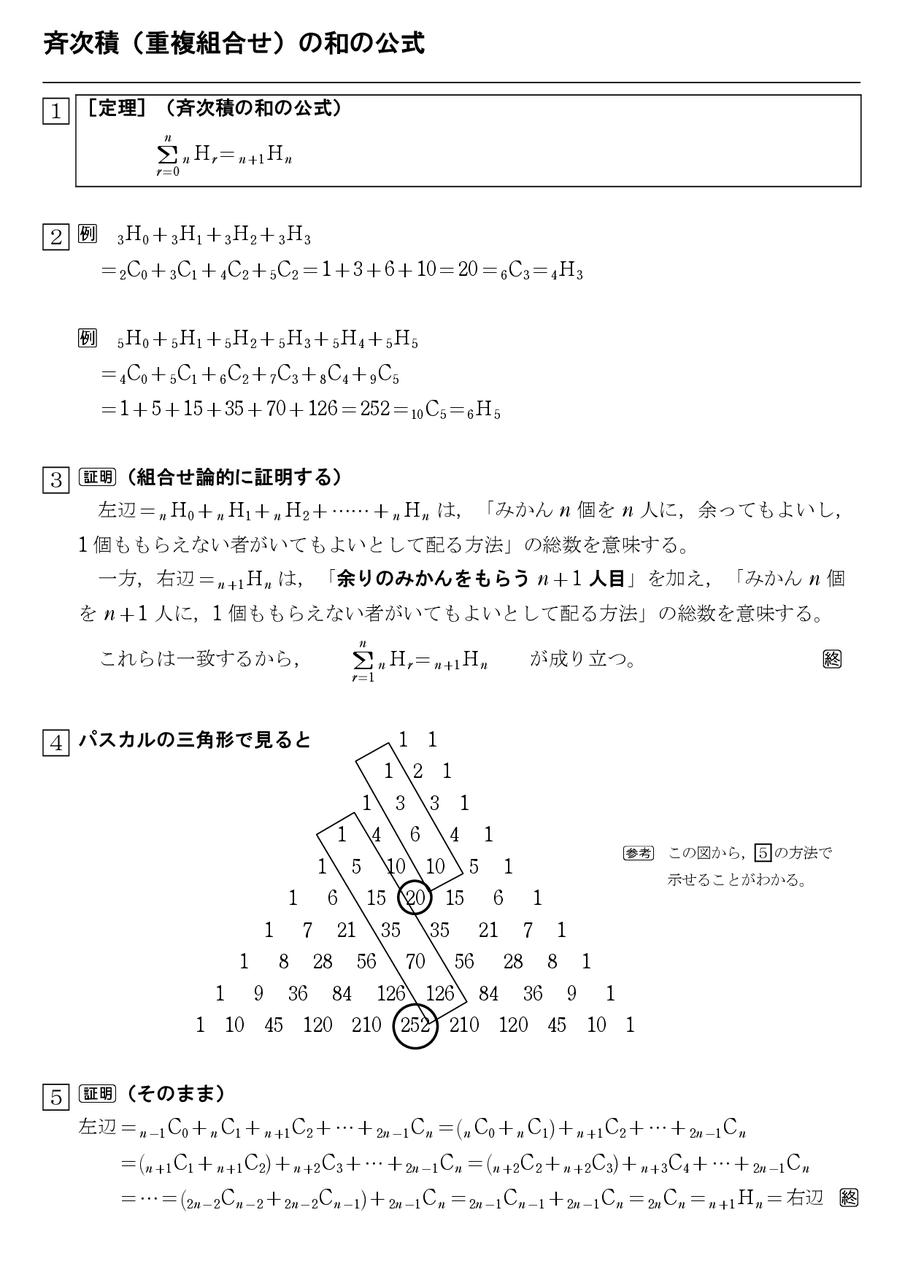
斉次積 重複組合せ の和の公式 怜悧玲瓏 高校数学を天空から俯瞰する

重複順列 Twitter Search Twitter

3

で囲ってあるところの考え方がわかりません Clearnote

順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ

理論編 重複組合せ とは 早大生の 省かない 数学

重複組み合わせ 重複組み合わせが分かりません なぜ異なるn個のもの Yahoo 知恵袋

なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ

順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ

重複組み合わせの公式と証明 簡単な計算方法 ビジュアル数学 数学ａ 場合の数

重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ

1

公式 組み合わせと順列の違い 見分け方 重複度を使う計算方法

重複組合せ

2

Incoming Term: 重複組み合わせ 公式, 重複組み合わせ 公式 なぜ, 重複組み合わせ 公式 使えない,